The Limits of Limits: Difference between revisions
(Created page with "'''Essay prompt''': Is the idea of 'limit' indispensable? Neutral? A hindrance? I contend that ''some'' concept of limit is indispensable in mathematics, but that one must be very cautious in using standard mathematics' concept of limit. The focus of this essay is mainly negative. I criticize two common attitudes towards limits: the "empiricist" attitude, which believes in effect that we don't need limits at all, and the "rationalist" attitude (the attitude of modern...") |
|||
| Line 3: | Line 3: | ||
I contend that ''some'' concept of limit is indispensable in mathematics, but that one must be very cautious in using standard mathematics' concept of limit. | I contend that ''some'' concept of limit is indispensable in mathematics, but that one must be very cautious in using standard mathematics' concept of limit. | ||
In this essay, I will criticize two common attitudes towards limits: the "empiricist" attitude, which believes in effect that we don't need limits at all, and the "rationalist" attitude (the attitude of modern mathematics), which believes that we can use limits without any thought as to how they connect to reality. Like ''epistemological'' empiricism and rationalism, the problem with these approaches is that the former overloads the crow through its use of percepts without concepts, and the latter floats up into the clouds through its use of concepts without percepts. What is needed is an ''objective'' view of limits. However, it is a very difficult task to lay out positive universal principles defining exactly what that objective view is, and so in this essay I will only attempt to sketch what it would be for two meager examples. | |||
== What is a limit? == | == What is a limit? == | ||
In this section, I will explain what a limit is. A limit can only be taken with respect to a ''sequence'', so first, I must explain what a sequence is. | In this section, I will explain what a limit is. I feel compelled to include this section, in part because this is advanced material and it has not been thoroughly discussed in class. A limit can only be taken with respect to a ''sequence'',<ref group="note">An objection I expect to hear is: don't we talk about things like "the limit as <math>x \rightarrow 0</math> of <math>f(x) := \sin(x)/x</math>"? My answer is that the way that that limit is found is by taking some sequence (any sequence) whose limit is 0, applying <math>f</math> to that sequence to get a new sequence, and then taking the limit of the new sequence. </ref> so first, I must explain what a sequence is. | ||
A sequence is a function<ref>A function is a quantitative relation between two groups of existents (called the "domain" and "codomain" of the function), which relates any existent in the domain to a ''unique'' existent in the codomain.</ref> from the natural numbers to a group <math>C</math> of existents, where there is some notion of ''closeness'' or ''distance'' between the units of <math>C</math>.<ref>Modern mathematics would say that <math>C</math> is a ''topological space'', but I do not wish to commit myself to that concept, because it raises potential philosophical problems. </ref> A sequence is like a set of instructions: you give me any natural number <math>n</math>, and I'll produce or identify some thing <math>a_n</math>, where <math>a_n</math> is a <math>C</math>. If | A sequence is a function<ref group="note">A function is a quantitative relation between two groups of existents (called the "domain" and "codomain" of the function), which relates any existent in the domain to a ''unique'' existent in the codomain.</ref> from the natural numbers to a group <math>C</math> of existents, where there is some notion of ''closeness'' or ''distance'' between the units of <math>C</math>.<ref group="note">Modern mathematics would say that <math>C</math> is a ''topological space'', but I do not wish to commit myself to that concept, because it raises potential philosophical problems. </ref> A sequence is like a set of instructions: you give me any natural number <math>n</math>, and I'll produce or identify some thing <math>a_n</math>, where <math>a_n</math> is a <math>C</math>. If a sequence consists of fractions with an inverse power of 10 in the denominator, then another way of thinking of that sequence is as instructions for continuing the "..." in a decimal expansion; the expression "3.14159..." can be thought of as shorthand for a specific sequence. Some examples of sequences: | ||
# "<math>a_1, a_2, a_3, \cdots </math>", where <math>a_n := \sum_{i = 1}^n 2^{-i}</math>. | # "<math>a_1, a_2, a_3, \cdots </math>", where <math>a_n := \sum_{i = 1}^n 2^{-i}</math>. | ||
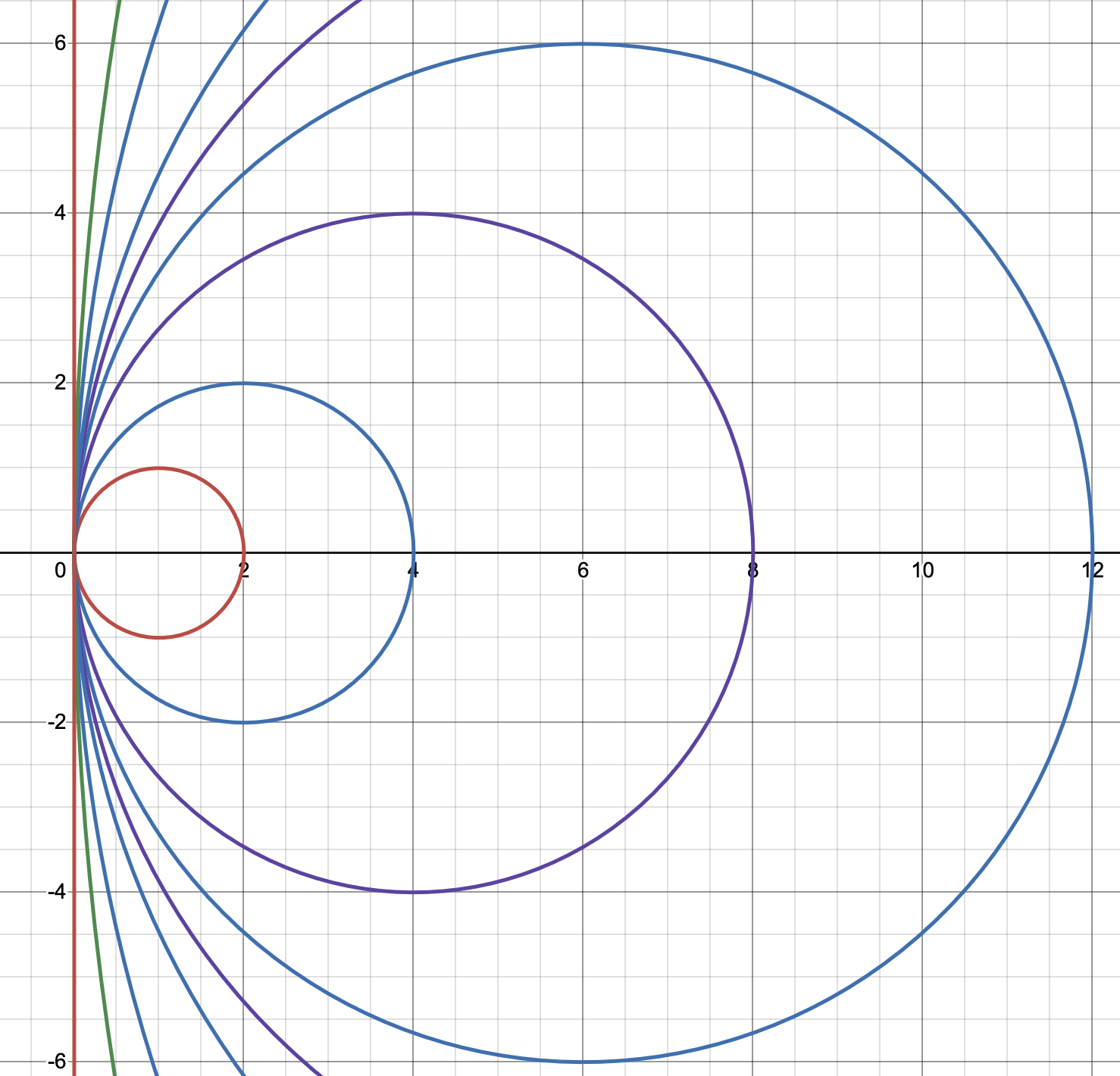
# "<math>b_1, b_2, b_3, \cdots </math>", where <math>b_n</math> is a circle of radius <math>n</math>, centered at <math>(x,y) = (n, 0)</math>. See | # "<math>b_1, b_2, b_3, \cdots </math>", where <math>b_n</math> is a circle of radius <math>n</math>, centered at <math>(x,y) = (n, 0)</math>. See figure 1. | ||
# "<math>c_1, c_2, c_3, \cdots </math>", where <math>c_n</math> is a secant line to the graph of <math>f(t) = 10-10 t^2 </math> near <math>t = 1</math>. More formally, <math>c_n</math> is the unique line passing through the points <math>\left(1 + 1/n, f(1 + 1/n) \right)</math> and <math> \left(1 - 1/n, f(1 - 1/n )\right)</math>. | # "<math>c_1, c_2, c_3, \cdots </math>", where <math>c_n</math> is a secant line to the graph of <math>f(t) = 10-10 t^2 </math> near <math>t = 1</math>. More formally, <math>c_n</math> is the unique line passing through the points <math>\left(1 + 1/n, f(1 + 1/n) \right)</math> and <math> \left(1 - 1/n, f(1 - 1/n )\right)</math>. | ||
# "<math>d_1, d_2, d_3, \cdots </math>", where <math>d_n := \log n</math>. | # "<math>d_1, d_2, d_3, \cdots </math>", where <math>d_n := \log n</math>. | ||
# "<math>e_1,e_2,e_3, \cdots</math>", where <math>e_n := \sum_{k = 0}^n \frac{(2k+1)!}{2^{3k+1} (k!)^2}</math>. | # "<math>e_1,e_2,e_3, \cdots</math>", where <math>e_n := \sum_{k = 0}^n \frac{(2k+1)!}{2^{3k+1} (k!)^2}</math>. | ||
[[File:Limit of circles.png|thumb|Circles of increasingly large radius becoming closer and closer to the vertical line on the left. ]] | [[File:Limit of circles.png|thumb|Figure 1. Circles of increasingly large radius becoming closer and closer to the vertical line on the left. ]] | ||
Sometimes, but not always, sequences have the property that the elements of the sequence get closer and closer to a fixed point <math>L </math> as the sequence progresses. In such cases, the sequence is said to converge to <math>L </math>, and <math>L </math> is said to be the limit of the sequence. Examples: | Sometimes, but not always, sequences have the property that the elements of the sequence get closer and closer to a fixed point <math>L </math> as the sequence progresses. In such cases, the sequence is said to converge to <math>L </math>, and <math>L </math> is said to be the limit of the sequence. Examples: | ||
| Line 21: | Line 21: | ||
# The circles "<math>b_1, b_2, b_3, \cdots </math>" gets closer and closer to being the y-axis (from the perspective of someone sitting at the origin), as <math>n</math> gets larger and larger. | # The circles "<math>b_1, b_2, b_3, \cdots </math>" gets closer and closer to being the y-axis (from the perspective of someone sitting at the origin), as <math>n</math> gets larger and larger. | ||
# The lines "<math>c_1, c_2, c_3, \cdots </math>" get closer and closer to being the tangent line to the graph of <math>f(t)</math> at <math>t=1</math>, as <math>n</math> gets larger and larger. | # The lines "<math>c_1, c_2, c_3, \cdots </math>" get closer and closer to being the tangent line to the graph of <math>f(t)</math> at <math>t=1</math>, as <math>n</math> gets larger and larger. | ||
# The numbers "<math>d_1, d_2, d_3, \cdots </math>" get larger and larger as <math>n</math> gets larger and larger. | # The numbers "<math>d_1, d_2, d_3, \cdots </math>" get larger and larger as <math>n</math> gets larger and larger. This sequence does not converge; it does not have a limit. | ||
# The sequence "<math>e_1,e_2,e_3, \cdots</math>" converges to <math>\sqrt{2}</math>.<ref>https://en.wikipedia.org/wiki/Square_root_of_2#Representations[TODO]</ref> That is, as <math>n</math> gets larger and larger, <math>e_n^2</math> gets closer and closer to 2. | # The sequence "<math>e_1,e_2,e_3, \cdots</math>" converges to <math>\sqrt{2}</math>.<ref>https://en.wikipedia.org/wiki/Square_root_of_2#Representations[TODO]</ref> That is, as <math>n</math> gets larger and larger, <math>e_n^2</math> gets closer and closer to 2. | ||
From these examples alone, it should be almost self-evident that some concept ''like'' a limit is indispensable. [TODO yuck] | |||
That is, each | == Example: converging to 1 == | ||
[[File:Pictorial proof of geometric sum.png|thumb|Figure 2. The design for the tile at the airport. White area represents places where there is to be granite, black area represents places where there is to be putty. ]] | |||
Look at the design shown in figure 2, and suppose that it is being proposed for some of the granite floor tiles at a new airport terminal. That is, each one of these floor tiles will consist of many sub-tiles, forming the pattern in figure 2. Each big tile is 1 square meter, so the sub-tiles have sizes 0.5 square meters, 0.25 square meters, etc. How much granite is needed to make each big tile? | |||
The answer to that question is perceptually obvious, given the picture of the design: about 1 square meter of granite is needed for each tile. But if what if we had to justify this to a blind person, or a person who hasn't seen the picture? | The answer to that question is perceptually obvious, given the picture of the design: clearly about 1 square meter of granite is needed for each tile. But if what if we had to justify this to a blind person, or a person who hasn't seen the picture? (Or, more importantly, what if we were in one of the innumerable situations which comes up in math and which is similar to this, but where no picture exists?) | ||
The empiricist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters, and if you perform a long arithmetic computation, you will find that <math display="block">\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \frac{1}{1024} = 0.9990234375,</math>which is close enough to 1 in the context at hand. Who cares about limits? | The empiricist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters, and if you perform a long arithmetic computation, you will find that <math display="block">\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \frac{1}{1024} = 0.9990234375,</math>which is close enough to 1 in the context at hand. Who cares about limits? | ||
The rationalist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters. The sequence of partial sums of these numbers is approximately the sequence <math>\{ a_n\} </math> (example 1 above). | The rationalist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters. The sequence of partial sums of these numbers is approximately the sequence <math>\{ a_n\} </math> (example 1 above). And the limit of that sequence is 1. Therefore, <math display="block">\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \frac{1}{1024} \approx 1 . </math>The advantage of the empiricist approach in this case is clear: it produces an answer which is correct, and we didn't have to leave reality at any point to get it. | ||
There are, however, some advantages of the rationalist approach. One advantage is that it doesn't involve any explicit computation, so it | There are, however, also some advantages of the rationalist approach. One advantage is that it doesn't involve any explicit computation, so it could save time and effort (especially in the days where people didn't have calculators). Another advantage of the rationalist approach is that it is more conceptual, and seems to give us a better idea about what's really going on: the sub-tiles form a pattern which, if continued in the natural way, would make their total area arbitrarily close to 1. In other words, the rationalist approach gives us some ''explanation'' for why the area of the sub-tiles is so close to 1. | ||
The problem with the rationalist approach is that, unlike the empiricist approach, its connection to reality is not obvious. What do we | The problem with the rationalist approach is that, unlike the empiricist approach, its connection to reality is not obvious. What do we mean by "approximately" when we say that "[t]he sequence of partial sums of these numbers is '''approximately''' the sequence <math>a_n</math> "? And in our conclusion that 1/2 + ... + 1/1024 ≈ 1, what do we mean by "≈", i.e. exactly ''how'' close can we conclude that 1/2 + ... + 1/1024 is to 1? | ||
To see a concrete way in which the rationalist approach can go awry, let's use the same logic and consider the sequence <math>a_1', a_2', a_3', \cdots </math>, where <math display="block">a_n' := \begin{cases} | To see a concrete way in which the rationalist approach can go awry, let's use the same rationalist logic and consider the sequence <math>a_1', a_2', a_3', \cdots </math>, where <math display="block">a_n' := \begin{cases} | ||
\sum_{i= | \sum_{i=1}^n 2^{-i}, &\text{if }n \leq 1000 \\ | ||
42, &\text{otherwise} | 42, &\text{otherwise} | ||
\end{cases}.</math>One might accidentally subsume 1/2 + ... + 1/ | \end{cases}.</math>One might accidentally subsume 1/2 + ... + 1/1024 under the sequence <math>\{a_n'\}</math> instead of the sequence <math>\{a_n\}</math>, because in reality we're only going up to <math>n = 10</math>, and these two sequences agree as long as <math>n \leq 1000</math>. The limit of the sequence <math>\{a_n'\}</math> is 42, so if one proceeded as before by taking the limit, he would erroneously conclude that <math display="block">\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} + \frac{1}{128} + \frac{1}{256} + \frac{1}{512} + \frac{1}{1024} \approx 42 . </math>Luckily, a more objective approach can be found by digging into the proof that the limit of <math>\{a_n\}</math> is 1. By basic algebra, one may verify that the following identity holds | ||
<math display="block">x + x^2 + \cdots + x^n = \left( \frac{1}{1 - x} - 1\right) - \frac{x^{n+1}}{1 - x}</math> | <math display="block">x + x^2 + \cdots + x^n = \left( \frac{1}{1 - x} - 1\right) - \frac{x^{n+1}}{1 - x}</math> | ||
for any number <math>x</math> such that <math>x\neq 1</math>. The term in parentheses should be thought of as a ''limit'', and the other term should be thought of as an ''error term'', or a deviation from the limit. Plugging in <math>x = 1/2</math>, the formula yields<math display="block">\frac{1}{2} + \frac{1}{2^2} + \cdots + \frac{1}{2^n} = 1 - \frac{1}{2^n},</math>so as <math>n</math> gets larger and larger, this quantity gets closer and closer to 1 (incidentally, that's the proof that the limit of <math>\{ a_n \}</math> is 1). In our case, <math>n = | for any number <math>x</math> such that <math>x\neq 1</math>. The term in parentheses should be thought of as a ''limit'', and the other term should be thought of as an ''error term'', or a deviation from the limit. Plugging in <math>x = 1/2</math>, the formula yields<math display="block">\frac{1}{2} + \frac{1}{2^2} + \cdots + \frac{1}{2^n} = 1 - \frac{1}{2^n},</math>so as <math>n</math> gets larger and larger, this quantity gets closer and closer to 1 (incidentally, that's the proof that the limit of <math>\{ a_n \}</math> is 1). In our case, <math>n = 10</math>, so the sum will be almost equal to the limit, but with an error of <math>1/2^{10}</math>, which is negligible for our purposes. Therefore we can conclude, rationally, that 1 square meter of granite is needed. | ||
Observe that in contrast to the empiricist approach, the objective approach didn't require a calculator, and it used concepts which clearly generalize far beyond the problem at hand. And in contrast to the rationalist approach, the objective approach produced a correct answer with a precise error bar, and didn't rely on any floating abstractions which could lead us down the wrong path. | |||
== Example: tangent lines == | |||
== | |||
In Boulder, Colorado, there is a street called Baseline that runs precisely along the 40th parallel—that is, the coordinate line at 40˚ north latitude. From my parents' house, Baseline stretches out to the east for many miles, and throughout entire length it runs along the 40th parallel. | In Boulder, Colorado, there is a street called Baseline that runs precisely along the 40th parallel—that is, the coordinate line at 40˚ north latitude. From my parents' house, Baseline stretches out to the east for many miles, and throughout entire length it runs along the 40th parallel. | ||
Revision as of 06:09, 22 August 2024
Essay prompt: Is the idea of 'limit' indispensable? Neutral? A hindrance?
I contend that some concept of limit is indispensable in mathematics, but that one must be very cautious in using standard mathematics' concept of limit.
In this essay, I will criticize two common attitudes towards limits: the "empiricist" attitude, which believes in effect that we don't need limits at all, and the "rationalist" attitude (the attitude of modern mathematics), which believes that we can use limits without any thought as to how they connect to reality. Like epistemological empiricism and rationalism, the problem with these approaches is that the former overloads the crow through its use of percepts without concepts, and the latter floats up into the clouds through its use of concepts without percepts. What is needed is an objective view of limits. However, it is a very difficult task to lay out positive universal principles defining exactly what that objective view is, and so in this essay I will only attempt to sketch what it would be for two meager examples.
What is a limit?
In this section, I will explain what a limit is. I feel compelled to include this section, in part because this is advanced material and it has not been thoroughly discussed in class. A limit can only be taken with respect to a sequence,[note 1] so first, I must explain what a sequence is.
A sequence is a function[note 2] from the natural numbers to a group of existents, where there is some notion of closeness or distance between the units of .[note 3] A sequence is like a set of instructions: you give me any natural number , and I'll produce or identify some thing , where is a . If a sequence consists of fractions with an inverse power of 10 in the denominator, then another way of thinking of that sequence is as instructions for continuing the "..." in a decimal expansion; the expression "3.14159..." can be thought of as shorthand for a specific sequence. Some examples of sequences:
- "", where .
- "", where is a circle of radius , centered at . See figure 1.
- "", where is a secant line to the graph of near . More formally, is the unique line passing through the points and .
- "", where .
- "", where .
Sometimes, but not always, sequences have the property that the elements of the sequence get closer and closer to a fixed point as the sequence progresses. In such cases, the sequence is said to converge to , and is said to be the limit of the sequence. Examples:
- The numbers "" get closer and closer to 1, as gets larger and larger.
- The circles "" gets closer and closer to being the y-axis (from the perspective of someone sitting at the origin), as gets larger and larger.
- The lines "" get closer and closer to being the tangent line to the graph of at , as gets larger and larger.
- The numbers "" get larger and larger as gets larger and larger. This sequence does not converge; it does not have a limit.
- The sequence "" converges to .[1] That is, as gets larger and larger, gets closer and closer to 2.
From these examples alone, it should be almost self-evident that some concept like a limit is indispensable. [TODO yuck]
Example: converging to 1
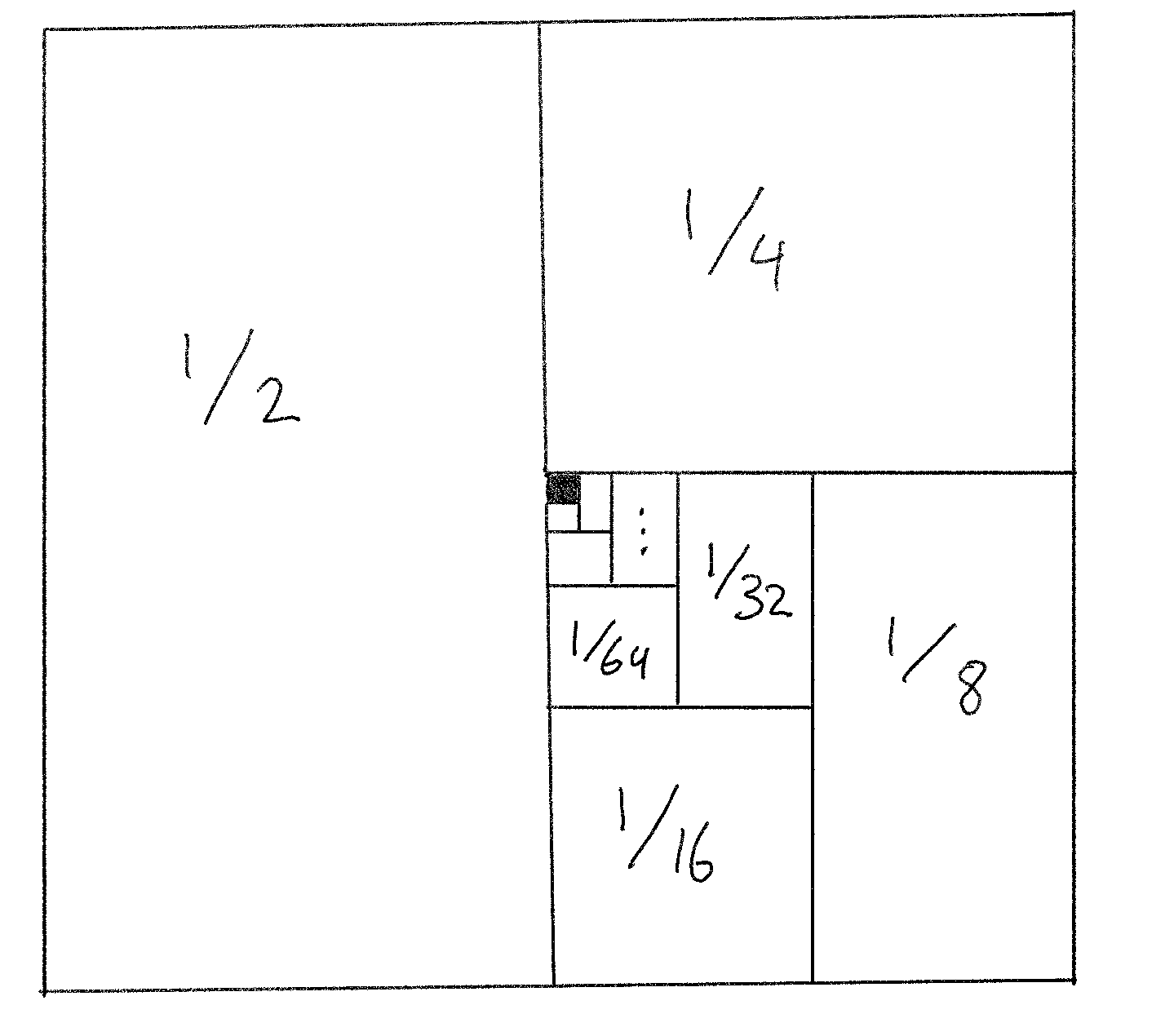
Look at the design shown in figure 2, and suppose that it is being proposed for some of the granite floor tiles at a new airport terminal. That is, each one of these floor tiles will consist of many sub-tiles, forming the pattern in figure 2. Each big tile is 1 square meter, so the sub-tiles have sizes 0.5 square meters, 0.25 square meters, etc. How much granite is needed to make each big tile?
The answer to that question is perceptually obvious, given the picture of the design: clearly about 1 square meter of granite is needed for each tile. But if what if we had to justify this to a blind person, or a person who hasn't seen the picture? (Or, more importantly, what if we were in one of the innumerable situations which comes up in math and which is similar to this, but where no picture exists?)
The empiricist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters, and if you perform a long arithmetic computation, you will find that
The rationalist way of proceeding would be to say: The big tile contains sub-tiles of sizes 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256, 1/512, and 1/1024 square meters. The sequence of partial sums of these numbers is approximately the sequence (example 1 above). And the limit of that sequence is 1. Therefore,
There are, however, also some advantages of the rationalist approach. One advantage is that it doesn't involve any explicit computation, so it could save time and effort (especially in the days where people didn't have calculators). Another advantage of the rationalist approach is that it is more conceptual, and seems to give us a better idea about what's really going on: the sub-tiles form a pattern which, if continued in the natural way, would make their total area arbitrarily close to 1. In other words, the rationalist approach gives us some explanation for why the area of the sub-tiles is so close to 1.
The problem with the rationalist approach is that, unlike the empiricist approach, its connection to reality is not obvious. What do we mean by "approximately" when we say that "[t]he sequence of partial sums of these numbers is approximately the sequence "? And in our conclusion that 1/2 + ... + 1/1024 ≈ 1, what do we mean by "≈", i.e. exactly how close can we conclude that 1/2 + ... + 1/1024 is to 1?
To see a concrete way in which the rationalist approach can go awry, let's use the same rationalist logic and consider the sequence , where
for any number such that . The term in parentheses should be thought of as a limit, and the other term should be thought of as an error term, or a deviation from the limit. Plugging in , the formula yields
Observe that in contrast to the empiricist approach, the objective approach didn't require a calculator, and it used concepts which clearly generalize far beyond the problem at hand. And in contrast to the rationalist approach, the objective approach produced a correct answer with a precise error bar, and didn't rely on any floating abstractions which could lead us down the wrong path.
Example: tangent lines
In Boulder, Colorado, there is a street called Baseline that runs precisely along the 40th parallel—that is, the coordinate line at 40˚ north latitude. From my parents' house, Baseline stretches out to the east for many miles, and throughout entire length it runs along the 40th parallel.
There is a fact familiar to every educated adult, that the Earth is a sphere, but that the radius of the sphere is so large that perceptually, to a person standing on the surface, it looks flat. This is an example of thinking of something as a limit; the plane is a limit of spheres of increasingly large radius. Similarly, any great circle on a sphere (such as the 40th parallel), in the limit that the radius of the sphere approaches "infinity," is a line (see the sequence above).
Now, consider the following very practical question, with a very obvious answer: If you start at my parents' house and walk east down Baseline for a mile, how far will you need to walk to return to my parents' house?
Empiricist approach: Well, okay, the 40th parallel is a circle on a sphere, and hmm let's see... the sphere has a very large radius... and so if you walk down this line... hmmm could there be a faster way to get back? I guess not because the radius is so large.
Rationalist approach: I passed to the limit, so really we are just considering a line in a plane. You're proposing to walk down a line in a plane, so obviously the shortest way back is to walk the same distance, in the opposite direction, down the same line. By the exact same logic, if you walked east down the 40th parallel for 20,000 miles, you'd have to walk 20,000 miles to get back.
The empiricist approach does not produce an incorrect answer, but it's a lot of unnecessary cognitive work, all done in some futile attempt to think of things "as they really are," and not make any simplifications using concepts. The rationalist approach gets the correct answer to the question asked, and it does so in a cognitively easy way, but it can go wrong because it's dropping context and disconnected from reality. (The italicized part of the rationalist's answer is wrong because if you travelled down the 40th parallel for long enough, you would end up back where you started, because the 40th parallel is a circle.)
The objective approach is to note that Boulder is very small compared to the area of the entire Earth, so it's okay to think of Boulder as a plane. You won't leave Boulder if you only walk for a mile, so this approximation remains valid for the scenario in question. Therefore, the (un-italicized part of the) rationalist reasoning applies: you'll have to walk 1 mile to return to my parents' house.
square root of 2
I don't have enough room to describe in detail a scenario in which the following might happen, but I claim that one runs into things like this all the time in mathematics and physics.
Suppose that I am doing some long computation, and involved somewhere in the computation is a square of area 2. At some point in the computation, I have to think about the side length of this square, which is √2. Then, even later in the computation, I have to square that side length, getting back to the square.
The math you should be writing down should look like
Notes
- ↑ An objection I expect to hear is: don't we talk about things like "the limit as of "? My answer is that the way that that limit is found is by taking some sequence (any sequence) whose limit is 0, applying to that sequence to get a new sequence, and then taking the limit of the new sequence.
- ↑ A function is a quantitative relation between two groups of existents (called the "domain" and "codomain" of the function), which relates any existent in the domain to a unique existent in the codomain.
- ↑ Modern mathematics would say that is a topological space, but I do not wish to commit myself to that concept, because it raises potential philosophical problems.








































