Continuity

Continuity is a concept denoting changes which do not happen very fast.

Objective Mathematics does not draw sharp distinctions between continuity and gradualness, nor does it draw sharp distinctions between discontinuity and abruptness. All four concepts are first-level concepts, that is, they directly identify percepts.

Whether a change is abrupt or gradual is a relative notion; a change may be identified as abrupt or gradual only when it is compared in consciousness to another change. In short, context matters. For example, in an everyday context, where one's point of comparison is days, hours, and minutes, the process by which a child grows into an adult is considered to be very gradual. By contrast, in a context where one is thinking about evolution by natural selection, i.e. where one's point of comparison is hundreds of millions of years, that same process is considered to be abrupt.

The traditional concept

What is the traditional concept of continuity?

It will be a long time before I write anything here. Go look it up. [TODO]

What is wrong with it?

The standard definition refers to real numbers, a concept which must be treated with care if one wants to preserve one's connection with reality.

As a result of its malformed concepts, the standard definition of continuity is not as practical as Objective Mathematics' definition. For example, consider the following two functions:

$f(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\0,&{\text{ otherwise}}\end{cases}}$,

$g(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\(x-0.99999999999)/0.00000000001,&{\text{ if }}0.99999999999\leq x<1\\0,&{\text{ otherwise}}\end{cases}}$.

In practice, there are many contexts where it is impossible to distinguish between these two functions. For example, an engineer whose ruler only goes down to 0.01 (in the appropriate units) would be completely unable to distinguish between them. Despite that, the formal math definition disregards context and always makes a sharp distinction between these two functions: $g$ is continuous, and $f$ is not.

This example could be much more drastic, for example instead of contrasting $f$ with $g$, I could have contrasted it with $h$, where

$h(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\(x-(1-\epsilon ))/\epsilon ,&{\text{ if }}(1-\epsilon )\leq x<1\\0,&{\text{ otherwise}}\end{cases}}$

and where $\epsilon$ is the reciprocal of 10^10^10^10^10. Quantities which are that small (in terms of non-pathological units) are very far outside the range of quantities that we expect might be measurable someday; it is physically impossible to distinguish between $f$ and $h$.

All of this proves that in real life, when given a function, it is never possible to tell if the function is continuous or not, according to the traditional definition of continuous. What's the point of having a concept if you can never actually use it to identify things in real life?

Analytic specification of continuity

Mathematics is the science of measurement, and so it should explain (or attempt to explain) precisely the measurements on which the proper concept of continuity is based. I will do that in this section, by giving a specification of continuity.

I will show how Objective Mathematics would treat continuity in the case of a function, $f:\mathbb {Q} \rightarrow \mathbb {Q}$.

Specification. Let $\nu :\mathbb {Q} _{>0}$ be the nill cutoff for the domain of $f$, and let $\rho :\mathbb {Q} _{>0}$ be the nill cutoff for the range of $f$. Then $f:\mathbb {Q} \rightarrow \mathbb {Q}$ is continuous if for all $a,b:{\text{im}}(f)$ such that $|a-b|>\rho$, any $\alpha :f^{-1}(a)$ and $\beta :f^{-1}(b)$ satisfy $|\alpha -\beta |>\nu$.

In plain English, the specification is saying that $f$ is continuous if any measurable difference between points in the range of $f$, comes from a measurable difference between points in the domain of $f$.

Requiring continuity seems to limit growth rates rather severely. An implication of this definition is that if $\rho =\nu$, then $f(x)=cx$ is continuous if and only if $-1\leq c\leq 1$. Since I don't have enough experience working with nill cutoffs, it is unclear to me whether or not that's a problem. It is certainly very different from standard mathematics.

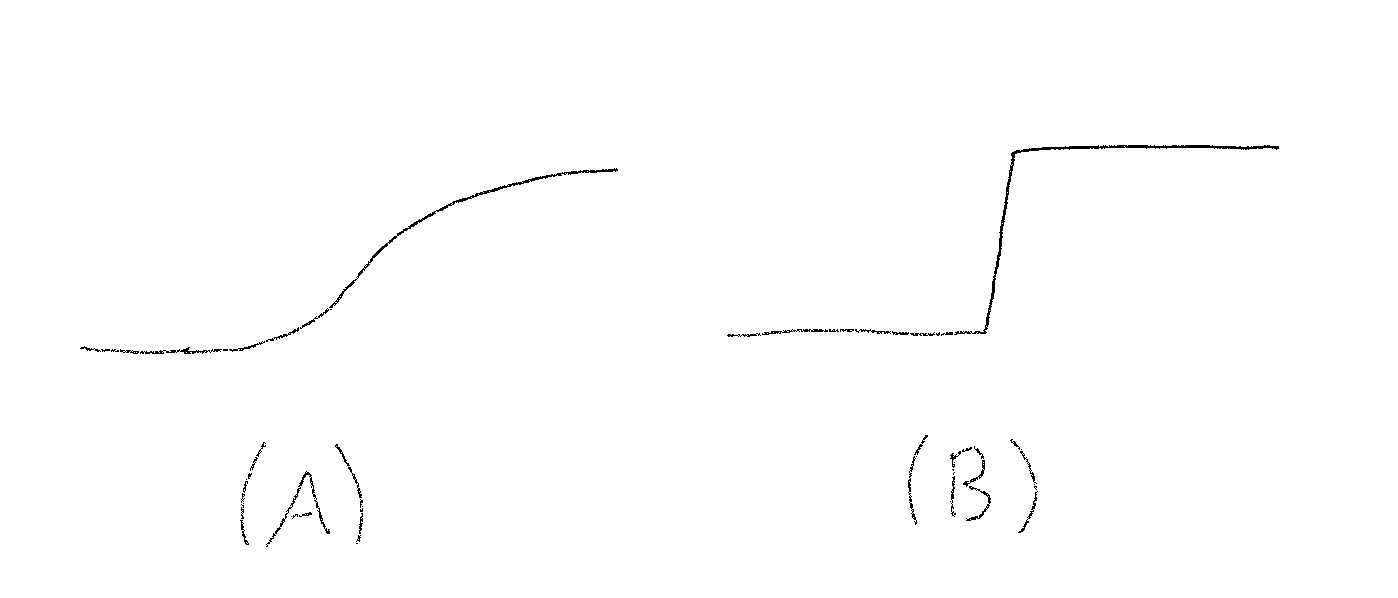
This is the "sharpest" possible definition of continuity. It does not capture all the ways in which the concept is used, e.g. figure 1.

Geometric specification of continuity

[TODO it will be a long time before I write anything here]

Examples

For a perceptual example, contrast the two images in figure (1). In comparison to (A), we identify that (B) undergoes an abrupt change of height; in comparison to (B), we judge that (A) undergoes a gradual change of height.

Figure 1: Moving from left to right, the height of (A) changes continuously, while the height of (B) changes discontinuously.

---

---

Rubber sheet geometry [TODO]

---

Knots [TODO]