Category theory: abstracting mathematical construction (essay)

Definition. A category ${\mathcal {C}}$ consists of the following data:

1. A class ${\text{ob}}({\mathcal {C}})$, called the "objects" of the category
2. For any two objects $X,Y\in {\text{ob}}({\mathcal {C}})$, a set ${\text{mor}}_{\mathcal {C}}(X,Y)$, called the "morphisms from $X$ to $Y$." We take $f:X\rightarrow Y$ to be a statement which means the exact same thing as the statement $f\in {\text{mor}}_{\mathcal {C}}(X,Y)$.
3. For any two morphisms $f:X\rightarrow Y$ and $g:Y\rightarrow Z$ , a function
   $$\circ :{\text{mor}}_{\mathcal {C}}(Y,Z)\times {\text{mor}}_{\mathcal {C}}(X,Y)\rightarrow {\text{mor}}_{\mathcal {C}}(X,Z),$$
   which we call "composition." That is, we can compose $f$ and $g$ to get an element $g\circ f:X\rightarrow Z$,

subject to the following conditions:

1. For any object $X\in {\text{ob}}({\mathcal {C}})$, there exists an "identity" morphism $1_{X}:X\rightarrow X$, satisfying $1_{X}\circ f=f$ for any $f:Y\rightarrow X$ and $g\circ 1_{X}=g$ for any $g:X\rightarrow Z$ .
2. Composition is associative: $(f\circ g)\circ h=f\circ (g\circ h)$.

♦

One example of a category---the example, in fact---is ${\text{Set}}$, the category of sets. The objects of ${\text{Set}}$ are sets, the morphisms of ${\text{Set}}$ are functions, and composition of morphisms of ${\text{Set}}$ is composition of functions: $(g\circ f)(x):=g(f(x)).$ The identity morphism of a set $X$ is the function $X\rightarrow X$ which does nothing.

Another example of a category is "the discrete category with 2 elements," which I shall call $\mathbb {I}$. The objects ${\text{ob}}(\mathbb {I} )$ are a set consisting of 2 elements (for concreteness we could take ${\text{ob}}(\mathbb {I} ):=\{a,b\}$ where $a=\emptyset$ and $b=\{\emptyset \}$). The morphisms of $\mathbb {I}$ are the identity elements, and nothing else. More formally, we have${\text{mor}}_{\mathbb {I} }(a,a)=\{*\}$, ${\text{mor}}_{\mathbb {I} }(a,b)=\emptyset$, and ${\text{mor}}_{\mathbb {I} }(b,b)=\{*\}$.

Another example of a category is the category ${\text{Grp}}$ of groups. Here, the objects are groups, and the morphisms are group homomorphisms.

Another example of a category is the (naive) category ${\text{Top}}$ of topological spaces. Here, the objects are topological spaces, and the morphisms are continuous maps.

We could go on like this ad infinitum. There are a huge variety of mathematical objects that form categories. Rings, graphs, vector spaces, representations, algebraic varieties, the points of the sphere, the open subsets of the plane, the natural numbers, compact Hausdorff totally disconnected spaces, etc etc. There is even a category ${\text{Cat}}$ whose objects are categories themselves. In fact, every mathematical object forms a category, though perhaps not in a useful way. Part of modern mathematical folklore is that you should always "categorify" whatever mathematical objects it is that you are working with, i.e. you should find a way to define everything in a category-theoretic way.

Note that the definition I gave of categories is set theoretic. Shea has reminded me that category theory can be taken as an alternative foundation to set theory (see here for Lawvere's attempt at that). I have barely studied Lawvere's ideas, but I am skeptical that it is useful as a foundation. One reason why is that when it comes to actually proving things, set theory is much easier than category theory, which wouldn't be the case if the latter was truly foundational (and hence integral to human thought). It has been my experience that even the most routine, "obvious" things can become very difficult to prove when phrased categorically. I don't think this is just my own ineptitude; I think there is a deep reason why category theory is difficult, which I will explain below. It's not just me, either: When working mathematicians want to understand something category theoretic, they often do things that allow them to think about it in a set theoretic manner, e.g. they embed their category into the category of sets (see "Yoneda embedding"), or choose a concrete set-theoretic model for their category.

Functors

I mentioned earlier that there is a category ${\text{Cat}}$ of categories. Clearly the objects of ${\text{Cat}}$ are ... categories, but what are the morphisms of ${\text{Cat}}$? They are called functors, and they are defined as follows.

Definition. A functor $F:{\mathcal {C}}\rightarrow {\mathcal {D}}$ is a function which sends any $X\in {\text{ob}}({\mathcal {C}})$ to an object $F(X)\in {\text{ob}}({\mathcal {D}})$, along with a function which sends any $\varphi \in {\text{mor}}_{\mathcal {C}}(Y,Z)$ to a morphism $F(\varphi )\in {\text{mor}}_{\mathcal {D}}(F(Y),F(Z))$. This assignment respects composition (meaning $F(\varphi \circ \psi )=F(\varphi )\circ F(\psi )$ for any morphisms $\varphi ,\psi$), and respects identity (meaning $F({\text{Id}}_{X})={\text{Id}}_{F(X)}$ for any object $X$). ♦

If you want examples of functors, you can find many of them in a category theory textbook. I will only give one example, one which I think demonstrates the essence and purpose of functors.

Let's suppose that we are mathematicians who wish to do some set-theoretic "construction." For example, one construction we could do is we could take any set $A$, and we could replace it with a set $A\sqcup A$, where $A\sqcup A$ is a set which has exactly two copies of every element of $A$. For example, if $A=\{a,b\}$ then we might have $A\sqcup A=\{(a,1),(b,1),(a,2),(b,2)\}$.

Now, let's suppose that we change $A$ in a "trivial" way. For example, instead of considering $A=\{a,b\}$, what if we considered $A'=\{a',b'\}$? Since $A$ and $A'$ are basically the same, nothing important would change. Instead of getting

$$A\sqcup A=\{(a,1),(b,1),(a,2),(b,2)\},$$

we would get

$$A'\sqcup A'=\{(a',1),(b',1),(a',2),(b',2)\},$$

which, again, is basically the same thing. Now, why am I entitled to say that $A$ and $A'$ are "basically the same," and that replacing $A$ with $A'$ was trivial? Because all I did was I took the contents of $A$, and I added a symbol ' to both of them! That's not interesting. More formally, I think that $A$ and $A'$ are "the same" because I have in mind a function $\varphi :A\rightarrow A'$, which sends $a\mapsto a'$ and $b\mapsto b'$, and this function is an isomorphism; it has an inverse function $A'\rightarrow A$ which sends $a'\mapsto a$ and $b'\mapsto b$ . Likewise, I think that $A\sqcup A$ and $A'\sqcup A'$ are "basically the same" because there is an isomorphism $A\sqcup A\rightarrow A'\sqcup A'$ sending $(a,1)\mapsto (a',1)$, $(b,2)\mapsto (b',2)$, etc.

It is clear that $A$ and $A'$ didn't play any special role in our construction; we could have done the exact same thing for any set $S$. Thus, for an arbitrary set $S$, let's define $F(S):=S\sqcup S$. Furthermore, let's call the latter isomorphism of the above paragraph $F(\varphi ):F(A)\rightarrow F(A')$. It's also clear that if $\psi :S\rightarrow T$ is any isomorphism of sets, then we get an isomorphism $F(S)\rightarrow F(T)$, sending $(s,i)\mapsto (\psi (s),i)$ which we shall call $F(\psi )$. Thus our construction defines a functor $F:{\text{Iso}}({\text{Set}})\rightarrow {\text{Iso}}({\text{Set}})$, where ${\text{Iso}}({\text{Set}})$ is that category whose objects are sets and whose morphisms are isomorphisms of sets. (Exercise: verify this last statement.)

Let's take a step back and observe what happened. We have a set-theoretic construction $S\mapsto S\sqcup S$. This set-theoretic construction is robust against arbitrary choices, in the sense that if we were to relabel all the elements of $S$ (that is, if we were to change $S$ to an isomorphic set $S'$), then there is an obvious way to relabel all the elements of $S\sqcup S$. This robustness means precisely that our construction defines a functor.

This, in my view, is the essence of functors. Functors represent mathematical constructions, such that when you make an unimportant change to the input of the construction, it induces an unimportant change on the output of the construction.

As any mathematician (or computer programmer) knows, whenever you are constructing something (or programming something), there are tons of details which are "arbitrary," in the sense that they that could have been other than the way they are. We even faced this issue in the previous section, when I defined the category $\mathbb {I}$. To define the objects of $\mathbb {I}$, I needed a set with two elements, and I chose ${\text{ob}}(\mathbb {I} ):=\{\emptyset ,\{\emptyset \}\}$. But I could just as well have chosen ${\text{ob}}(\mathbb {I} ):=\{\{\emptyset \},\{\{\emptyset \}\}\}$, or ${\text{ob}}(\mathbb {I} ):=\{1,2\}$, or ${\text{ob}}(\mathbb {I} ):=\{*,\star \}$, or anything else, and it wouldn't have made a big difference: The resulting category would have been essentially the same. (Likewise, when programming a computer, it doesn't matter if we begin our for-loops at 0 and end at n-1, or begin them at 1 and end them at n: The resulting computer program will be essentially the same.)

Functors are a way of talking about constructions, that abstracts away the arbitrary choices that went into the construction. Functors gain their "independence" from arbitrary choices because to build one, you have to say how it would handle any possible arbitrary choice. Here we also see why category theory is difficult: saying how you would handle any possibility is much more difficult than just saying how you would do the construction in one specific case.

Universal properties

Besides functors, there is another way in which categories abstract away from arbitrary choices, called "universal properties."

The construction (or as we now know, the functor) $S\mapsto S\sqcup S$ of the previous section suggests a more general construction. Given two sets $A:=\{a,b\}$ and $B:=\{\alpha ,\beta ,a\}$, we can construct their disjoint union

$$A\sqcup B:=\{(a,1),(b,1),(\alpha ,2),(\beta ,2),(a,2)\}.$$

This should be contrasted with the union of $A$ and $B$, $A\cup B:=\{a,b,\alpha ,\beta \}$. The disjoint union keeps the $a\in A$ separate from the $a\in B$, and the union does not. Disjoint union and union are different concepts. In standard set theory, the union is taken to be an axiomatic notion, and the disjoint union is taken to be a construction.

Given any set $S$ and any set $T$, we can construct a set $S\sqcup T$ whose elements are the elements of $S$ and the elements of $T$. More formally,

Definition. The disjoint union of a set $S$ and a set $T$ is the set

$$S\sqcup T:=\{(x,i)\ |\ (x\in S\wedge i=1)\vee (x\in T\wedge i=2)\}.$$

♦

It is possible to get at the exact same idea in a way which is differs in mere technical details. We could instead have defined the disjoint union as

$$A+B:=\{(1,2,a),(1,2,b),(3,4,\alpha ),(3,4,\beta ),(3,4,a)\},$$

and generally,

Definition. The disjoint sum of a set $S$ and a set $T$ is the set

$$S+T:=\{(i,j,x)\ |\ (x\in S\wedge i=1\wedge j=2)\vee (x\in T\wedge i=3\wedge j=4)\}.$$

♦

It is clear that the thing I'm calling "disjoint union" and the thing I'm calling "disjoint sum" are not different in an important way. Both of them capture the idea that, given two sets, there exists a set which has all the elements of the first one and all the elements of the second one, and which keeps the elements separate. The "disjoint union" construction keeps $a\in A$ separated from $a\in B$ by putting the former into a tuple with "1", and putting the latter into a tuple with "2". The "disjoint sum" construction reverses the order, and keeps $a\in A$ separated from $a\in B$ by putting the former into a 3-tuple with "1" and "2", and putting the latter into a 3-tuple with "3" and "4".

We see that there is something arbitrary about the details of these constructions. What is the common essence that disjoint union and disjoint sum share, which we are trying to capture with our formal definitions? Is it even possible to talk about such a thing mathematically? The answer to the latter question is yes(!!), and the answer to the former question is that these two constructions possess the same universal property. I will not try to define this concept yet, but rather I will proceed inductively by studying the disjoint union and disjoint sum in greater depth.

The first thing to note about the disjoint union is that there is always an "inclusion" function $i_{S}:S\rightarrow S\sqcup T$ sending $s\mapsto (s,1)$, and an "inclusion" function $i_{T}:T\rightarrow S\sqcup T$ sending $t\mapsto (t,2)$. These data possess the following property:

Proposition 1 (universal property of the coproduct). For any set $X$, and any functions $\lambda _{S}:S\rightarrow X$, $\lambda _{T}:T\rightarrow X$, there exists a function $\chi :S\sqcup T\rightarrow X$ such that $\chi \circ i_{S}=\lambda _{S}$ and $\chi \circ i_{T}=\lambda _{T}$, and $\chi$ is the unique function with this property. More formally, uniqueness means that if there is any function $f:S\sqcup T\rightarrow X$ such that $f\circ i_{S}=\lambda _{S}$ and $f\circ i_{T}=\lambda _{T}$, then necessarily $f=\chi$. ♦

This proposition is logically somewhat complex ($\forall \exists \forall$), but the reader will find that it is very easy to prove once he gets a grip on what it is saying.

The more standard and succinct (but less clear) way to state the above proposition would be to say "for any set $X$, and any functions $\lambda _{S}:S\rightarrow X$, $\lambda _{T}:T\rightarrow X$, there exists a unique function $\chi :S\sqcup T\rightarrow X$ such that $\chi \circ i_{S}=\lambda _{S}$ and $\chi \circ i_{T}=\lambda _{T}$." But rather than writing out that long sentence every time, a category theorist would draw the following diagram:

The universal property of the coproduct.

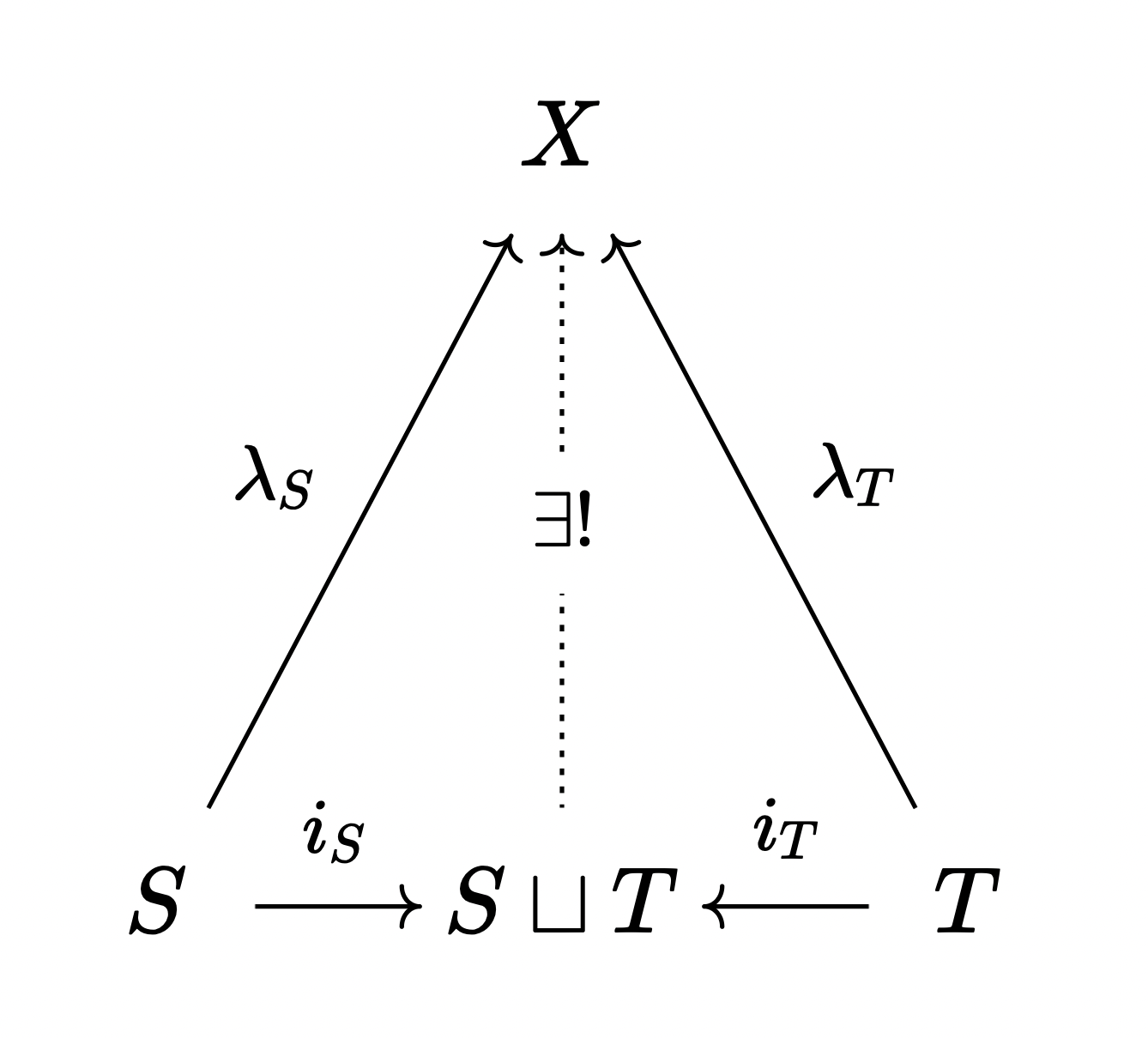
The universal property of the coproduct is also satisfied by the disjoint sum. That is,

Proposition 2. For any set $X$, and any functions $\lambda _{S}:S\rightarrow X$, $\lambda _{T}:T\rightarrow X$, there exists a function $\chi :S+T\rightarrow X$ such that $\chi \circ i_{S}=\lambda _{S}$ and $\chi \circ i_{T}=\lambda _{T}$, and $\chi$ is the unique function with this property. More formally, uniqueness means that if there is any function $f:S+T\rightarrow X$ such that $f\circ i_{S}=\lambda _{S}$ and $f\circ i_{T}=\lambda _{T}$, then necessarily $f=\chi$. ♦

Note that this "universal property of the coproduct" is entirely category theoretic: to state the property, you don't have to know any of the details about what's inside $X$, $S$, or $T$, and you don't have to know anything about what the functions $i_{S}$, $\lambda _{T}$, etc. are doing. You don't even have to know that $X$, $S$, and $T$ are sets, and that $i_{S}$, $\lambda _{T}$, etc. are functions. For the statement to make sense, we just have to know that $X$, $S$, and $T$ are objects in some category, and that $i_{S}$, $\lambda _{T}$, etc. are morphisms in that category.

A consequence of this generality is that we could have formulated the exact same universal property in any other category, whether it be groups, topological spaces, natural numbers, or anything else. There's no guarantee that any object of a given category will actually possess this property, but one could state it nonetheless. In particular, if there were a different category of sets from the standard one (and I alluded to the fact that I think there ought to be a better one), then this property would still make sense. Another consequence of this generality is the following:

Proposition 3. Let $S$ and $T$ be two objects of any(!) category, and suppose that $S\rightarrow Y\leftarrow T$ and $S\rightarrow Z\leftarrow T$ both satisfy the universal properties of the coproduct. Then $Y$ and $Z$ are uniquely isomorphic(!).

As an exercise, the reader should give a more precise statement of proposition 3 (i.e. state precisely what "uniquely isomorphic" means), and prove it.

Corollary of proposition 3. The disjoint sum and disjoint union of $S$ and $T$ are uniquely isomorphic.

This is the sense in which the disjoint sum and the disjoint union are really "the same" construction! They satisfy the same universal property, and therefore are isomorphic in a canonical way.

I can now give a definition of a universal property. A universal property is a property possessed by an object of a category, which characterizes it up to a canonical/unique isomorphism. Besides the coproduct, there are many other familiar sets and set-theoretic constructions that possess universal properties, for example, the product of two sets $S\times T=\{(s,t)\ |\ s\in S,t\in T\}$, a set containing a single element $\{*\}$, a coproduct of three sets $S\sqcup T\sqcup R$, and anything else that you can dream up. For an example of the flavor of universal products in other categories, I shall note that in many geometrical categories (where the objects are shapes / spaces of some sort), the (transverse) intersection of two objects satisfies a universal property (the universal property of the pullback), and the gluing together of two objects satisfies a universal property (the universal property of the pushforward).

In conclusion, with universal properties we observe the same phenomenon that we observed with functors. There are some arbitrary details in our math constructions, but this concept helps us talk about our math constructions in a way which guarantees that those arbitrary details won't matter. If the only properties of $A\sqcup B$ that we ever use are those that follow from its universal property, then it is completely indistinguishable from $A+B$. Of course, just like for functors, this robustness against arbitrary choices comes at the cost of making category theory more difficult than set theory: instead of just writing down a set and chugging along, we have to learn and automatize a complicated $\forall \exists \forall$ statement.

Conclusion (general relativity and beyond)

This theme of canonical math constructions, i.e. those which can be performed without making any choices, is very powerful. I believe that the ideas of category theory will have implications that go far beyond the ridiculously abstract fields (algebraic geometry, homotopy theory) in which they are presently employed. I will conclude with just one tantalizing example:

The laws of classical mechanics are formulated with respect to coordinate systems. A coordinate system is a choice, which could have been otherwise: the 0˚ longitude line could have been just as easily defined to run through Paris as it was defined to run through Greenwich. If your coordinate system is changed drastically, then the form of the laws of classical mechanics change drastically in turn. For example, if your coordinate system is rotating, then there is a Coriolis force.

One might ask the question: How do we formulate the laws of physics in a way so that they look the same, regardless of what coordinate system we are using? I suspect that in answering that question, you will arrive at something like General Relativity.