Continuity

Continuity is a concept denoting changes which do not happen very fast.

Objective Mathematics does not draw sharp distinctions between continuity and gradualness, nor does it draw sharp distinctions between discontinuity and abruptness. All four concepts are first-level concepts, that is, they directly identify percepts.

Whether a change is abrupt or gradual is a relative notion; a change may be identified as abrupt or gradual only when it is compared in consciousness to another change. In short, context matters. For example, in an everyday context, where one's point of comparison is days, hours, and minutes, the process by which a child grows into an adult is considered to be very gradual. By contrast, in a context where one is thinking about evolution by natural selection, i.e. where one's point of comparison is hundreds of millions of years, that same process is considered to be abrupt.

The traditional concept

What is the traditional concept of continuity?

It will be a long time before I write anything here. Go look it up. [TODO]

What is wrong with it?

The standard definition refers to real numbers, a concept which must be treated with care if one wants to preserve one's connection with reality.

As a result of its malformed concepts, the standard definition of continuity is not as practical as Objective Mathematics' definition. For example, consider the following two functions:

$f(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\0,&{\text{ otherwise}}\end{cases}}$ ,

$g(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\(x-0.99999999999)/0.00000000001,&{\text{ if }}0.99999999999\leq x<1\\0,&{\text{ otherwise}}\end{cases}}$ .

In practice, there are many contexts where it is impossible to distinguish between these two functions. For example, an engineer whose ruler only goes down to 0.01 (in the appropriate units) would be completely unable to distinguish between them. Despite that, the formal math definition disregards context and always makes a sharp distinction between these two functions: $g$ is continuous, and $f$ is not.

This example could be much more drastic, for example instead of contrasting $f$ with $g$ , I could have contrasted it with $h$ , where

$h(x)={\begin{cases}x,&{\text{ if }}x\geq 1\\(x-(1-\epsilon ))/\epsilon ,&{\text{ if }}(1-\epsilon )\leq x<1\\0,&{\text{ otherwise}}\end{cases}}$

and where $\epsilon$ is the reciprocal of 10^10^10^10^10. Quantities which are that small (in terms of non-pathological units) are very far outside the range of quantities that we expect might be measurable someday; it is physically impossible to distinguish between $f$ and $h$ .

All of this proves that in real life, when given a function, it is never possible to tell if the function is continuous or not, according to the traditional definition of continuous. What's the point of having a concept if you can never actually use it to identify things in real life?

Analytic specification of continuity

Mathematics is the science of measurement, and so it should explain (or attempt to explain) precisely the measurements on which the proper concept of continuity is based. I will do that in this section, by giving a specification of continuity.

I will show how Objective Mathematics would treat continuity in the case of a function, $f:\mathbb {Q} \rightarrow \mathbb {Q}$ .

Specification. Let $\nu :\mathbb {Q} _{>0}$ be the nill cutoff for the domain of $f$ , let $\rho :\mathbb {Q} _{>0}$ be the nill cutoff for the range of $f$ , and let $\lambda :\mathbb {Q} _{>0}$ . Then $f:\mathbb {Q} \rightarrow \mathbb {Q}$ is $\lambda$ -continuous if for all $a,b:{\text{im}}(f)$ such that $|a-b|\geq \rho$ , any $\alpha :f^{-1}(a)$ and $\beta :f^{-1}(b)$ satisfy $|\alpha -\beta |\geq \lambda \nu$ .

In plain English, the specification is saying that $f$ is continuous if any measurable difference between points in the range of $f$ , comes from a measurable difference between points in the domain of $f$ . One could have called this a specification of " $(\rho ,\nu ,\lambda )$ -continuity," since it depends on $\rho$ and $\nu$ , but I did not do that because $\rho$ and $\nu$ are fixed by the instruments of measurement. [TODO isn't $\lambda$ also fixed by the instruments of measurement? what does $\lambda$ mean conceptually?]

Note that unlike the traditional definition of continuity, $\lambda$ -continuity is actually measurable: you could verify that a real-life function is or is not $\lambda$ -continuous [modulo concerns about not being able to measure every single fraction. But I don't think that's important; just choose an interval]. The algorithm to do this is: make a ruler shaped like $\sqsubset$ , where the lines on the bottom and top have length $\rho$ , and the line on the left has length $\lambda \nu$ . Now run the bottom left corner of the ruler along your graph, being careful to keep the bottom of it parallel to the x axis. If the graph ever goes through the top right corner, then it is discontinuous. If not, then it is continuous.

Requiring continuity seems to limit growth rates rather severely. An implication of this definition is that if $\rho =\nu$ , then $f(x)=cx$ is $\lambda$ -continuous if and only if $-1/\lambda \leq c\leq 1/\lambda$ .^{[note 1]}

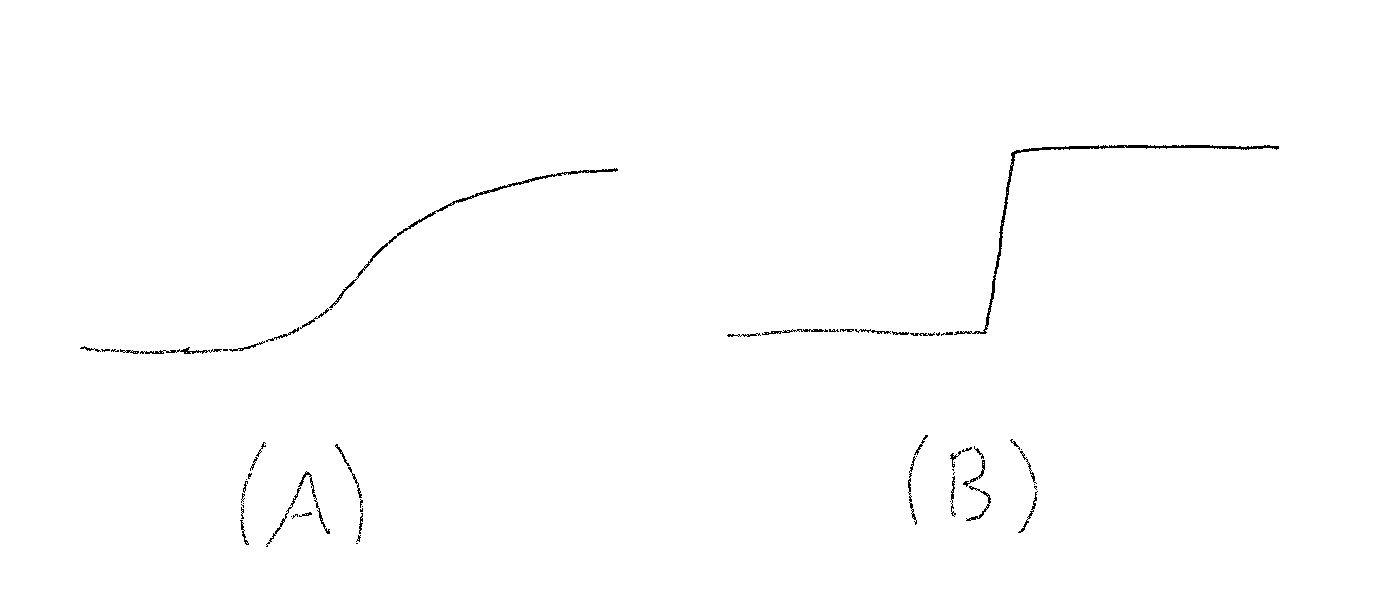
To use this definition to distinguish the cases (A) and (B) of figure (1), we should choose a model for figure (1). Let $f_{A}(x)=\tan ^{-1}(x)$ , and

f_{B}(x)={\begin{cases}-1,&{\text{ if }}x\leq 0.1\\10x,&{\text{ if }}-0.1\leq x\leq 0.1\\1,&{\text{ otherwise}}\end{cases}}

and suppose that the nill cutoff in the domain is equal to the nill cutoff in the range. The slope of

f_{A}

is only

\geq 1

at a single point, so it is 1-continuous, whereas

f_{B}

is not. [TODO work out in detail?]

Geometric specification of continuity

[TODO it will be a long time before I write anything here]

Examples

For a perceptual example, contrast the two images in figure (1). In comparison to (A), we identify that (B) undergoes an abrupt change of height; in comparison to (B), we judge that (A) undergoes a gradual change of height.

Figure 1: Moving from left to right, the height of (A) changes continuously, while the height of (B) changes discontinuously.

---

Rubber sheet geometry [TODO]

---

Knots [TODO]

Notes

↑ Proof. This is trivial when $c=0$ , so suppose otherwise. Suppose that $|c|\leq 1/\lambda$ . Then for any $a,b:\mathbb {Q}$ , if $|a-b|\geq \rho$ , then $|f^{-1}(a)-f^{-1}(b)|={\frac {|a-b|}{|c|}}\geq {\frac {\rho }{|c|}}\geq \lambda \rho$ so $f$ is $\lambda$ -continuous. Conversely, suppose $f$ is $\lambda$ -continuous. Choose $a,b:\mathbb {Q}$ such that $|a-b|=\rho$ . Then by continuity $|f^{-1}(a)-f^{-1}(b)|\geq \lambda \rho$ , or equivalently $\rho /|c|=|a-b|/|c|\geq \lambda \rho$ , or equivalently $|c|\leq 1/\lambda$ . $\square$

[1] Proof. This is trivial when $c=0$ , so suppose otherwise. Suppose that $|c|\leq 1/\lambda$ . Then for any $a,b:\mathbb {Q}$ , if $|a-b|\geq \rho$ , then $|f^{-1}(a)-f^{-1}(b)|={\frac {|a-b|}{|c|}}\geq {\frac {\rho }{|c|}}\geq \lambda \rho$ so $f$ is $\lambda$ -continuous. Conversely, suppose $f$ is $\lambda$ -continuous. Choose $a,b:\mathbb {Q}$ such that $|a-b|=\rho$ . Then by continuity $|f^{-1}(a)-f^{-1}(b)|\geq \lambda \rho$ , or equivalently $\rho /|c|=|a-b|/|c|\geq \lambda \rho$ , or equivalently $|c|\leq 1/\lambda$ . $\square$

[note 1]

Continuity

Contents

The traditional concept

What is the traditional concept of continuity?

What is wrong with it?

Analytic specification of continuity

Geometric specification of continuity

Examples

Notes

Navigation menu

Continuity

The traditional concept

What is the traditional concept of continuity?

What is wrong with it?

Analytic specification of continuity

Geometric specification of continuity

Examples

Notes

Navigation menu

Search