E

e is a [TODO]

Probabilistic interpretation

Bernoulli trials

Suppose that something has a 1 in $n$ chance of occurring. After $n$ times, what is the probability that the event has not happened once? Each time, the probability that the event doesn't happen is $(1-1/n)$, so the probability that the event doesn't happen $n$ times in a row is $(1-1/n)^{n}$.

It turns out that this sequence is Cauchy [TODO], and $e$ is the inverse of its limit

$${\frac {1}{e}}:=\lim _{n\rightarrow \infty }\left(1-{\frac {1}{n}}\right)^{n}.$$

Similarly, if something has a 1 in $n$ chance of occurring, then after $nt$ times, what is the probability that the event has not happened once? For large $n$ it approaches some fixed value

$$e^{-t}=\lim _{n\rightarrow \infty }\left(1-{\frac {1}{n}}\right)^{nt}.$$

The[TODO terminology] numerical value of e is useful to know, because if you're ever in a situation where you have to calculate one of these probabilities, it could be a major pain to multiply $(1-1/n)$ with itself $nt$ times, if you had no access to a calculator. Instead, you could save yourself some work by looking up this number[TODO it's not a single number; it's a sequence of numbers] $e$ in a table that someone has already computed. [TODO I don't find this explanation very convincing.]

Central limit theorem [TODO]

Suppose you do $N$ experiments, where in each experiment you flip a coin 100 times and record the results. For $0\leq k\leq 100$, what fraction of the experiments resulted in heads landing precisely $k$ times?

For $N$ large, the answer is proportional to

$$e^{-(k-50)^{2}/\sigma }$$

for some constant $\sigma$.

Compounding interest interpretation [TODO yuck]

If you have your money in a bank account, where you make a rate of interest $r$, which compounds $c$ times yearly, then after a year your bank account will contain

$$(1+r)^{c}$$

times your principal. Now suppose that it compounds many times ($c$ is large), but the interest $r$ is small. Fix the rate to be $r=1/c$, then we are interested in what the multiplier $(1+1/c)^{c}$ is when $c$ is very large. It turns out to converge to some constant

$$e:=\lim _{c\rightarrow \infty }\left(1+{\frac {1}{c}}\right)^{c}$$

This example, though it's how e is introduced, is rather disconnected from reality. No bank actually offers this as an option. And even if they did, why would they fix the rate to be $r=1/c$? Why not some other rate? [TODO the answer, I think, is that if $r(c)$ grows faster than $1/c$ then the limit will diverge, and if it grows slower than $1/c$ then the limit will be 1.]

Geometric interpretation

" A ray through the unit hyperbola x² − y² = 1 at the point (cosh a, sinh a), where a is twice the area between the ray, the hyperbola, and the x-axis. For points on the hyperbola below the x-axis, the area is considered negative" [TODO]

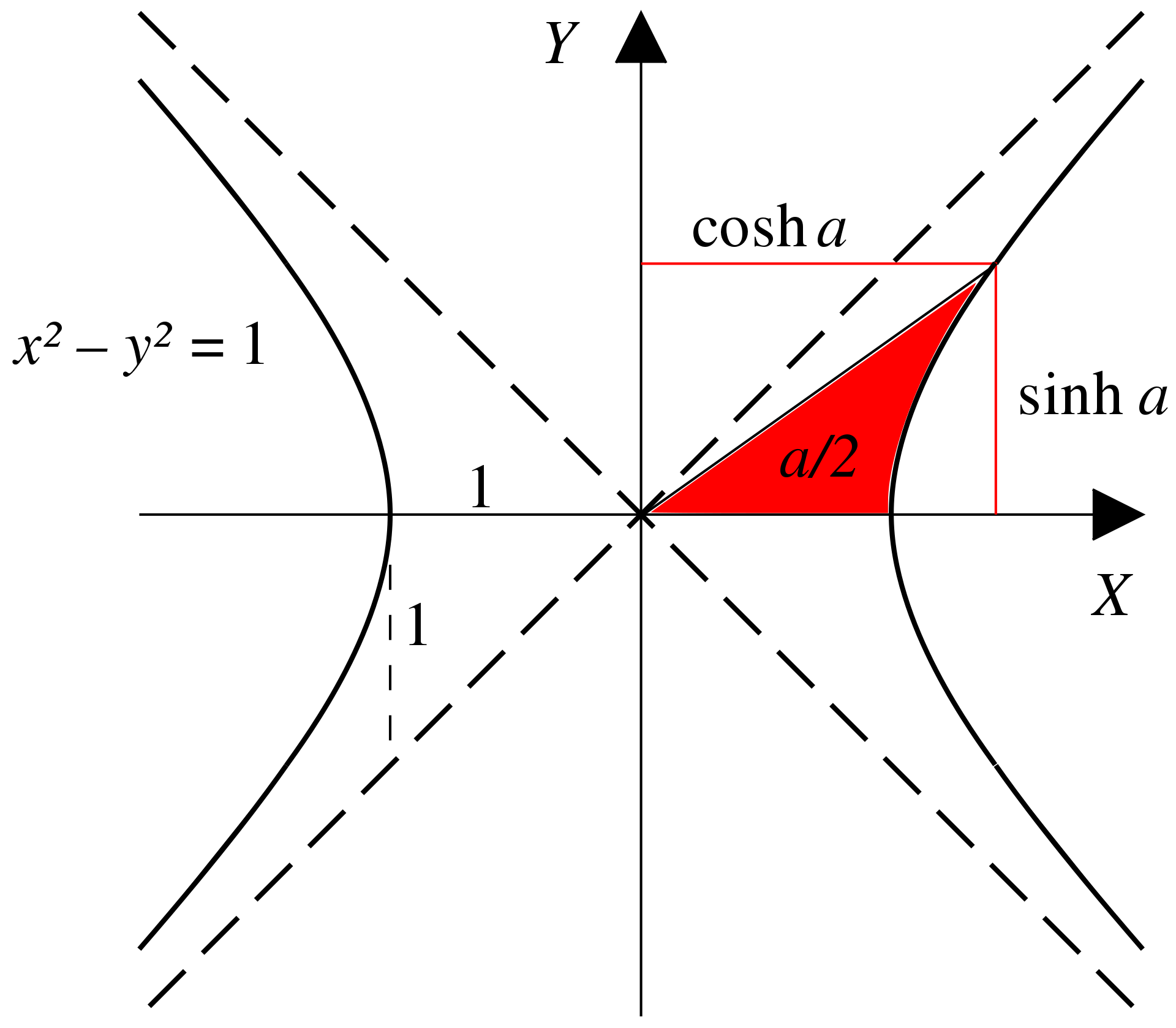
$\cosh(a)$ and $\sinh(a)$ are the $x$ and $y$ coordinates on a unit hyperbola, at the place where the ray subtending an area of $a/2$ intersects the hyperbola. (This description is not very clear; see the figure.) In this situation, $e^{a}$ is the simply sum of $x$ and $y$ coordinates.